Harp project summary

By Scot Gresham-Lancaster

Preface:

This document summarizes the current state of a decades long line of research regarding the invention of a new type of music controller. This controller has gone through several versions and prototypes but all the investigations share the common thread: investigating a three dimensional relationship between solid struts and strings under tension.

What follows is a transcription from a web page that outlined some of the history of this project up until 2001,

http://www.o-art.org/Scot/Tensegrity.html

The Tensegrity Harp Project

Scot Gresham-Lancaster ongoing research ( since 1983 ) into the harmonic relationships suggested by the geodesic, synergetic, and tensegrity math of R. Buckminster Fuller.To See the lastest update click here

Early in 1983 I was commissioned to write the music for a wedding reception of performance artist and art curator Evan Painter. At that time I was steeped in reading Synergetics by Buckminster Fuller and decided to work with these mathematics as a compositional determinate. I was particularly interested at that time, in the vocabulary of the geodesic dome that described the rational relationship of the length of strut members in a geodesic object as "Chord" factors. This obvious allusion to harmonic relationships prompted me to create a piece that mapped these specific frequency relationships determined by the lengths of an architectural structure to a harmonic lattice. These harmonic lattices are common among researchers in to intonation theory and so I based the research on combining my knowledge of geodesic math with the concepts of harmonic lattices put forward in modern intonation theory. My first project involved using the lattice created using the chord factors from a 6 frequency geodesic ellipsoid with foci proportioned at the golden mean. If the great ellipse of the defined structure was 2 units across, the distance between the foci would be 1.61803989... units ( the golden mean ). The lattice of chord factors that construct such a geodesic ellipsoid will generate. The main attribute of the lattice is that it is described by a triangular juxtaposition of members as opposed to the quadrille or quadrilateral displacement of Cartesian based mathematics.

By multiplying each of the chord factors of the representative architectural strut members by the fundamental frequency of the intended scale the frequency relationship of each chordal member is established. These chord derived frequency sets are ordered in matrices based on each struts placement in the original structure. By collecting the parameters of adjacent matrix members to the in ordered grouping, isorhythmic chord groupings and polyphonic melodies determined by these relationships are generated. This complex set of predetermined systems generated a sweet and pleasing sound field that had inherent symmetries of motion and confluence and yet was complex enough to afford continuous gentle variation.

The sequential playing of groupings in the matrices could actually be visualized as planes that were passing through the ellipsoid. Sticking strictly to these intersections as a means of timing lead to thinking of the vertices of the structure as being "strings" of a conceptual harp that was being played by the planes as they passed through each vertices. truncated octahedron tensegrity This concept of the vertices being strings, led to the next phase of the research. This type of structures based on the work of Kenneth Snelson lent itself to being the basis for a playable instrument appeared to be the tensegrity structures. The question was how was this new proposed instrument to sound: acoustically or in more challenging way as a means of playing the multiple parameters needed for the control of digital synthesis algorithms. By transducing the net stress of each of the faces of a tensegrity structure ( such as the truncated octahedron in the illu. ) then one could intuitively control multiple parameters associated with processes such as vocoding, re-synthesis, etc. Also, if one could distinguish between the act of stretching and the act of plucking, more useful musical information would be generated by the instrument. This intuitively interesting project is fraught with technical difficulties, however.

AppleMark The problems associated with the work are both of a hardware and software nature. Additionally, there are considerations that add to the look of the instrument as an aesthetically beautiful object. A transducer was needed that would translate the information regarding the stretching and plucking of the suspension members without interrupting the look of the instrument. My association with STEIM and its cadre of instrument designers lead me to many potential solutions. First Bert Bongers suggested a transducer that was linked to a spring that was in a machined part that held a magnet and a hall effect sensor. This is a problematic solution mostly because of the non-linearity of the hall effect sensor. In thinking about the problem more carefully, I came across al line of inquiry that seemed very interesting.

In electronics magazines I spotted a company called Instrument Specialties Inc.. which specialized in making special purpose gaskets for electromagnetic isolation of components in microwave electronics. One of their products was called "Conductive Silicon Elastomers". The short description included the information that the material could be doped with carbon, copper, aluminum, nickel, etc. It occurred to me if this string like material was stretched that there was a chance that the metal particles suspended in the silicon would contact more their changing any resistance that was created. Upon talking to the field representatives this was indeed the case. I then went over the specification sheets and selected the carbon/nickel combination as having the best conductivity with at least some resistivity. After some phone work I was able to acquire a six foot sample of a fabricated 130 mm length of this material. It met and exceeded my expectations. At rest it has almost no resistivity with about 100 ohms at 12 cm. when stretched this resistance increases linearly with stretch to about 4 M ohms. This was quite good for my purposes.

By using this material with a voltage across the members of a tensegrity structure can be connected to an A/D converter and the stretch can be congruently converted into a digital number based on the resolution and sampling rate of that conversion. With the backing of the Multimedia masters degree program at CSUHayward and the support of Microchip Inc. I have acquired a PicMaster emulator and a Picstart plus programmer. For my initial experimentation, I am using the PIC 16C77 embedded processor which has integrated into it eight 8 bit A/D channels. With this system I can read the stretching of the structure and in that way create a dynamic vector model that can be remapped to abstract parameters associated with one or many DSP algorithms that are generating, delaying, filtering or in some other way modyifying sonic material.

The most, initially, unclear aspect of the reason for this construction can be summed up in a historical perspective of my experiences with various types of alternative controllers.

Postscript July 11, 2001: Last night while watching the PBS series "Building Big" there was an interview with sculptor and designer Kenneth Snelson in which it was revealed that R Buckminister Fuller should not be attributed with the actual conceptualization of the tensegrity structure, but rather blatantly took credit for work that Mr. Snelson had done. This sort of robbing of attribution is something that has plagued my own work as a technical assistant and digital music problem solver for many years and so I was very embarrassed when in my excitement at discovering this fact I wrote to Mr. Snelson without taking the time to edit this page to reflect this truth. Those who are interested are invited to read a full account of a corrected history in the form of a letter to R. Motro of the International Journal of Space Structures by Mr. Snelson that sets the record straight.

Update from February 2002

I have decided to take another approach on the construction of this instrument and not use the Conductive Silicon Elastomers. While they produced promising results they were not stable and required constant recalibration. I spent more time on the recalibration routines than working on the routines to make the construction a viable musical instrument. So there are now two prototypes using two different approaches.

One is based on the Tensegritoy model. (http://www.neurotoys.com/tensg.html )

By building this model I was given an elastic version of the structure I intended to work with then I simply attached linear potentiometers to the members and took the output of those potentiometers directly into a voltage to midi conversion box (the STEIM sensorlab ) and input the midi conversion into a Macintosh computer running Max software. I use Max to message the data for the particular application that I am working on.

The second model is more elaborate. I built struts out of oak and mounted guitar tuning machines on one end and added a bridge on the other. Then i constructed a real stringed harp using the tension created by the tuning pegs to tighten and tune up the construction. This phase is now finished and I have what i would describe as a multi dimensional Berimbau. The next phase of the building of this instrument is to add six single coil pickups to the bridge of each of the struts and then not only amplify the unique string vibration and sounds that they produce, but also do a real time spectrum analysis and general acoustical analysis of each of the pickups and use that as a performance determinate. I am currently working on the best pickups and mountings for those pickups on the instrument.

Unfortunately there are no photos of these 2 prototypes. A student was using the model that was just described during a demonstration in a class of mine at CSUH in Nov. of 2001 and he handled it too roughly and broke a string. Since the entire structure is held together by integrated “tensegrity”, the whole instrument fell apart. This pointed out a here to fore unrealized and very major flaw with this design approach; if a string breaks the entire instrument simply disintegrates into a heap of wires and sticks. This required rethinking the entire approach to the instrument. One of the other reoccurring problems was that if none of the struts touched then each of the tensions nodes would need to wirelessly transmit the information form each end of the strut. This was also a major technical issue since then the instrument would need at least 12 independent wireless channels or some form of 12 channel multiplexing that would take the current/resistance reading at each vertex with an A/D converter, encode that information and wirelessly transmit it to the central processing unit. This would require a significant modification to the existing STEIM sensor lab that was being used since it had no wireless capabilities other than ultrasound up to that point. We did spend one afternoon trying to multiplex ultra sonic bursts from a mockup of the vectors, but it was to fraught with errors from echoes and other acoustic interference.

Third Prototype the Octahedral Harp

At this point the experience of the use of tensegrity and the problems that it produced lead to the next design idea. Unnamed for many months as we worked on prototypes it came to be called the Octahedral harp. 6 vertex and 12 edges for 12 separate resonating strings.

Here is a picture of me holding the second prototype at STEIM in the Netherlands in 2002 taken by may collaborator on that project instrument builder and master electronic music instrument builder Jorgen Brinkman.

It was made of oak struts with guitar tuners on each vertex. The center is a custom built brass armature that tightens into brass sleeves with a locking screws. In this pass on the technology we hacked a Logitech Rumblepad ® to act as a wireless data acquisitions source. The new library of HID libraries implemented by STEIM as a package called Junxion that takes the USB signal from any interface device and remaps it to any number of the many midi controller parameters.

In the summer of 2002 we developed the first working prototype of this instrument.

This sketch shows many of the various attributes of the actual physical design. It includes a sketch of the laser harp assembly and the location of the modified Logitech unit, the FM transmitter and the Force Sensing resistors. The laser harp assembly is diffraction of a single laser through a series of 6 glass slices all equidistant from each other at a 45-degree angle. This sends 6 equidistant beams at each photo resistor along the vertical strut online.

The handle is form fit with divits. Within these impressions, force sensing resistors are mounted. In this way the performer has independent control of parameters via each finger tip. There are two thumb switches and a thumb pad that is also an FSR.

It was discovered that the resonance the strings conducted through each of the struts. By mounting piezo elements on either side of the main horizontal strut. The stereo FM transmitter in the sketch is one of those units produced to connect an iPod or CD Walkman to an FM radio in a car stereo. So the range is limited to about 12 feet or so.

This picture illustrates the interconnections available to the wireless joystick control. There are two joysticks and two sliders for a total of 10 independent 0-5V inputs. Also, with the D-control pad and the various other switches there is a total of 4x4 grid or 16 on of switches.

There are three separate strings that cross four bridges on each of the three axis, XYZ. This makes 12 isolated courses for a single string based instrument. Each of these three courses of strings on each axis are electrically isolated. By pulsing each string with a heterodyning pulse burst, they each become alike a Theremin. The picture to the left, on the top is a signal without the heterodyning of a buddy near the string and so 3 of the switch inputs can read the pulses and give information that is analogous to the proximity.

The initial idea was to use this controller solely as a live multi-parameter electro-acoustic control device, but at this evolution of the instrument the piezo provided an interesting acoustic element that had not been anticipated. If it was to be developed that way one would need to get independent electrical coil pickups on each of the 12 courses to get the individual frequency for each independent string fragment.

At this point in the experimentation it became clear the intonation of each of these strings needed to be more carefully considered. The first assumption was that by making the proportions of the struts whole number ratios with each other the intonation would fall in place. Of course, this was not well thought out since the strings define the hypotenuse of a triangle. So the frequency was congruent with the square root of the addition of to just lengths, which was some irrational proportion that was very nearly impossibly out of tune. So with the help of shaman performance artist Sam Ashley, we developed a Max patch to try and discover a tuning proportion

This method relied entirely on a heuristic approach and while interesting as a stand alone interest, proved useless for the over all arc of this project.

4^th Prototype 2004

Eleven years into the project and it was substantially a completely different endeavor. The concept of a direct link to the ideas of Snelson and Fuller had given way to an entirely new conception that was really more about the functionality of the proposed instrument. Two major developments occurred in the fall of 2004 that made an impact of the design of the 4^th prototype. While working at CNMAT on a video project for composer Edmund Campion, I began having a series of extended conversations with Adrian Freed the amazing Technical Director there. He was working quite closely with composer Roberto Gonzalez on a new electro acoustic harp which was modeled on the diatonic harps of Latin America. Much like the diatonic CelticHarps of Ireland these Peruvian and Mexican harps had the traditional design that one sees with a harp, but Adrian had discovered if he put some piezo film under the straddle of each srting he could directly read the fundamental frequency and amplitude of a plucked string. This was an amazing bit of technological information for my work since I had a total of 24 bridges to work from. The comparison of the phase and frequency of the piezo on each end of a given string length could be analyzed to also give the position where the string was plucked. I incorporated those electronics into the next phase of the design.

So to recap the features:

Twelve independent strings

Kynar piezo pickups on each bridge

i. Transduces string vibration to voltage

ii. Time comparison algorithm to locate position of pluck or bow

Motorola MC33794 chip generates a 3-D electrical field and detects the size and shape of objects within the field and is attached to each of the independent 3 strings.

Low wattage laser diffracted through 6 glass sides at a 45 degree angle point at photoreceptors that vary in voltage based on light blockage

This design was presented to the CREATE studio at UCSB in 2003. Here is the talk announcement from that event:

OCTOBER 17, 2003, AT 4 PM.

HUMAN CONSIDERATIONS FOR MAKING MUSIC WITH MACHINES

Location

Music Dept., Room 2215 (Studio Xenakis)

The lecturer will present his current work in developing a multi dimensional controller specifically designed for the live execution of electro acoustic music. The "Tensegrity Harp" integrates 42 channels of control and 4 acoustic information channels with the specific intent that this information be used to shepherd digital sound production and sound processing algorithms.

Is breath any longer necessary? : Human considerations for making music with machines.

The rhetorical question in the title points up the danger imposed by the integration of technology in the act of making music. As the act of making music becomes more and more integrated with automated processes and discorporate transducers and interfaces, will music change in the face of no longer being integrated with the performer/composers body in any tangible way?

Also, he will discuss the social ramifications of using broadband networks, such as Internet2, for creating new social music making contexts that integrate visual and sonic immersive techniques to collapse two or more geographically separated performance space into one shared performance space.

Finally, he will discuss the relationship of ubiquitous computing and the phenomenon of smart/flash mobbing to the future of performance practice, and the long term ramifications of the integration of technology into future performance practices.

http://www.create.ucsb.edu/create/createWeb/news/newsShow.php?id=30

Working with my friend Jon Steele in Oakland we made another protoype that used Brazilian hard wood and Upright bass strings. That instrument was much like the one designed at STEIM with one major difference : the vertex or bridges were done at the end of the struts and not with pass through holes like in the previous model. This precluded the need for the slightly heavy brass center piece. However, intonation was still a problem. Here is a picture of that instrument:

Insert picture here:

The main discovery with this instrument was that it was very difficult to isolate the resonance of a separate string length and therefore the idea of cueing the location of the string excitation from the time difference between the two bridges was often confused. Particularly when the harp was played polyphonically. For more information on this technique refer to:

http://citeseer.ist.psu.edu/paradiso02passive.html

After building this fourth harp it became clear that there was a need to completely solve the intonation problem associated with the proportions of the struts. It finally and rather obviously became clear that the problem needed to be addressed from another perspective. Rather than solving for the adjacent and opposite of the various right triangles defined by this structure, what was needed was to set the hypotenuses to the various desired whole number ratio lengths and then calculate the lengths of the three struts from there.

Unfortunately, this proved to be a much more involved problem that first anticipated. To prove that it was near possible a model was created that had 12 independent pieces of 1/4 inch dowel with Velcro on each end. These dowels were cut to this proportion.

len["AF"] = 6.0 / 5.0;

len["FB"] = 15.0 / 8.0;

len["BE"] = 9.0 / 5.0;

len["EA"] = 1.0;

len["CF"] = 4.0 / 3.0;

len["FD"] = 8.0 / 5.0;

len["DE"] = 3.0 / 2.0;

len["EC"] = 5.0 / 4.0;

len["AC"] = 9.0/ 8.0;

len["CB"] = 5.0 / 3.0;

len["BD"] = 2.0/ 1.0;

len["DA"] = 16.0/ 15.0;

Using this rather crude method, it was determined that there was a good chance that a set of strut lengths could be found that would create a set of 12 edges on an irregular octahedron that would have this particular set of ratios on each edge. Finding thus specific strut lengths was made difficult by only having one side and an angle given.

Here is a rendering of the approximate relationships of each of these edges.

The next pass on this was to figure a method to make this determination. I turned to my friend and long time collaborator Dr. William Thibault of the CSUEastBay Math and Computer Science Department. He had recently been working with Genetic algorithms to solve the problems associated with automatically aligning multiple projectors for seamless surround projection. If interested go to: http://obscuradigital.com for more information. He surmised that he could use these same genetic algorithms to determine a best fit for creating accurate strut lengths for such a just intoned theoretical object. Here is the latest code that he developed in collaboration with the author to try and solve this problem. It requires a library called the Real Genome from MIT to properly compile.

Click on this link to see the code that was developed by Bill Thibault for this Purpose

Alarmingly, this code returned no actual solution. Of interest to any math students reading this is that there may be no solution to this seemingly very straightforward problem

Genetic algorithm solution for AB CD EF

	X	Y	Z
Origin	0	0	0
A	-0.3273	5.35152	1.30954
B	1.68074	-9.1841	1.3938
C	-6.45179	0.90998	-7.89049
D	1.83111	-0.929835	9.0854
E	-3.54813	1.43955	-1.08322
F	9.70693	-5.55459	1.02791

String Length	Meters	Feet decimal	feet	inches	fraction
ACBD =	5.858	19.21916013	19	2	5/8
AFBE =	5.875	19.27493441	19	3	5/16
CEDF =	5.683	18.64501315	18	7	3/4

Strut Length
AO =	0.53272	1.747769032	1	9	0	8.973228346
BO =	1.68074	5.514238854	5	6	3/16	0.170866142
AB =	2.21346	7.262007885	7	3	1/8	3.144094488
CO =	0.90998	2.985498692	2	11	13/16	11.82598425
DO =	0.929835	3.050639768	3	0	5/8	0.607677165
CD =	1.839815	6.036138461	6	0	7/16	0.433661417
EO =	1.08322	3.553871396	3	6	5/8	6.646456693
FO =	1.02791	3.372408142	3	4	1/2	4.468897638
EF =	2.11113	6.926279538	6	11	1/8	11.11535433

These solutions were within 1 mm or so, but the error is about 3 to cycles. In reality, however, with adjustable bridges and other adjustments, this is a very workable set of measures. It is of intellectual interest that there is not a “perfect” solution to this three dimensional problem, however.

Once a solution was in place a new extension came to mind.

Next Phase: the 72 course Octahedral Harp

The idea arose to extend the number of strings on each axis from 1 to 6, using guitar hardware at each of the vertexes Here is a sketch

There would be a total of 72 independent string lengths with a total of 18 strings; 6 strings on each axis. The concept would be for there to have each set of strings to be set to just pentatonic scale. Below is a table of the resultant frequencies of mapping the 12 edge frequencies to the most common just pentatonic frequency set. These combinations of ratios result in some repeated ratio combinations -

1000= 1/1 9/8 - 5/4 - 3/2 - 5/3 – 2/1

1/1 1000.000-1125.000-1250.000-1500.000-1666.667-2000.000

15/16 1066.667-1200.000-1333.333-1600.000-1777.778-2133.333

9/8 -1125.000-1265.625-1406.250-1687.500-1875.000-2250.000

6/5 -1200.000-1350.000-1500.000-1800.000-2000.000-2400.000

5/4 -1250.000-1406.250-1562.500-1875.000-2083.333-2500.000

4/3 -1333.333-1500.000-1666.667-2000.000-2222.222-2666.667

3/2 -1500.000-1687.500-1875.000-2250.000-2500.000-3000.000

8/5 -1600.000-1800.000-2000.000-2400.000-2666.667-3200.000

5/3 -1666.667-1875.000-2083.333-2500.000-2777.778-3333.333

9/5 -1800.000-2025.000-2250.000-2700.000-3000.000-3600.000

15/8 -1875.000-2109.375-2343.750-2812.500-3125.000-3750.000-

2/1 -2000.000-2250.000-2500.000-3000.000-3333.333-4000.000-

Color Key

Single Frequency No highlight = 23 solo

Pair of Frequencies Yellow Highlight = 9 pairs

Three Frequencies Green Highlight = 3 trios

Four Frequencies Blue Highlight = 4 quads

Five Frequencies Grey Highlight = 1 set of 5

This then indicates that there would not be 72 distinct frequencies on the harp but rather a total of 40 distinct frequencies present. This is significant because if the instrument was used solely to trigger electro acoustic events that would mean that would mean that 40 not 72 separate events could be detected by frequency alone. Of course using the acoustic distance detection algorithm in conjunction with the frequency mapping on the three dimensional object could possibly give a 3d mapping of the performers gestures on the instrument.

As with much of the process of creating the early prototypes, each new phase creates a new set of potential new means of expression for to investigate.

Since the genetic algorithm was unable to map the end points exactly to the whole number ratio set that we were initially inputting a new strategy to be able to adjust these frequencies is needed. The previous illustration shows the strings being bridged at a square roughly near each vertex. The idea in that case is to take advantage of electric guitar hardware at the bridge points. A standard adjustable bridge would easy in fabrication and give the advantage of being able to make fine adjustments to compensate for the 1- 2 % error that the genetic algorithm generated. Another approach is to crat a more “harp-like” configuration using concentric octahedral string distributions with each congruent configuration being scaled by the degree of the just pentatonic or even larger (diatonic, 2 octave pentatonic or diatonic etc.) scale. This sketch may give the reader an idea about such a configuration.

While only two of the twelve edges are represented in this sketch the orientation in this “congruent” configuration is somewhat more like a standard harp configuration. The main disadvantage is that each of the vertex would require special fabrication for the adjustable bridges needed to bring each of the edge lengths fully into tune.

Conclusion … ?

At this point, the next phase of the project is waiting on sufficient funds to make the 5^th and possibly sixth prototype that can be used to examine the issues regarding the construction of the full realization of this generation of this ongoing project. Perhaps the most interesting outcome of this ongoing research has been the evolution that each of the various stages of research have been forced on the development not by conjecture but by the reality of trying to make the physical models of these rather abstract concepts. The act of realization is enlightening as the actual physical model and the procedures needed to create this model create special requirements that can not be predicted and have always lead to new conclusions and lines of inquiry.

In a perfect world research like this could be evenly and consistently be followed to logic conclusions in controlled and well-funded circumstance. However, these prototypes have each been surprisingly expensive. The last full realization of the octahedral harp was well over $300 in parts cost alone. Using Brazilian hardwood for the lengths ($75), new bass strings ($120), and professional quality tuners for the three string courses ($72). One can see by expanding this to 72 courses or 18 strings at anywhere near these costs that the raw materials alone are near $1000. This fact alone has stopped the progress of fully realizing this next generation of prototyping. However, work has started on and experimental prototype with aluminum angle and piano wire more as a feasibility study and to investigate the actual intonation of the harp as predicted by the genetic algorithms.

This has been an exciting if very slow moving process, but soon a new instrument will emerge that shares an ancient lineage and portends the best use of new technologies in an attempt to create a focused instrument that is designed specifically for the promise of purely digitally generated sound material.

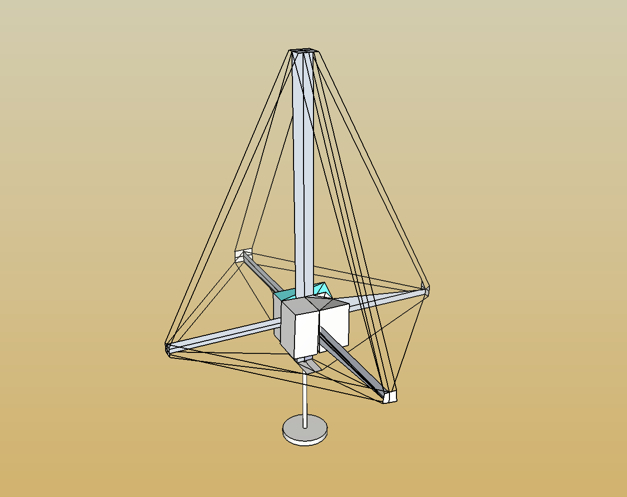
Here is a shot of a sketchup rendering of my current thinking on the design.

octehedral harp